Il sistema che viene chiamato:
- La ruota di Lorenz

E' quello che illustra meglio l'andamento dell' attrattore di Lorenz

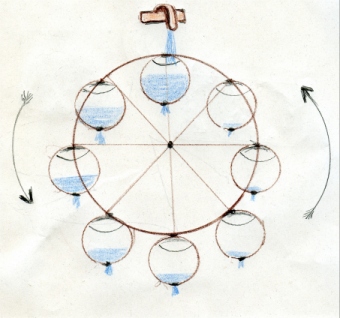
La figura che vedi qui sopra a sinistra è un disegno che mostra il funzionamento del sistema.

Su una rota vengono sistemati dei contenitori con un foro sul fondo, sopra la ruota un rubinetto aperto fa entrare l'acqua nel contenitore un cima alla ruota.

Se dal rubinetto esce poca acqua, il contenitore non riesce a riempirsi, perchè l'acqua esce da foro sul fondo, in questo modo il sistema non si muove.

Se dal rubinetto esce una maggiore quantità di acqua, il foro nel contenitore non riesce a smaltire l' acqua in tempo, perciò riesce a riempirsi e con il suo peso comincia a far girare la ruota, in questo modo il contenitore che lo segue si riempie a sua volta dando inizio ad un andamento stabile del sistema, la ruota gira finchè l'energia fornita (la quantità dell'acqua) rimane stabile.

Se però facciamo uscire ancora più acqua dal rubinetto, i contenitori si riempiono più velocemente e la ruota girando ad una maggiore velocità non lascia uscire abbastanza acqua dal fondo del contenitore, in questo modo il peso eccesivo rallenta la risalita del contenitore e il moto della ruota, che ad un certo punto può ridiscendere e tornare sui suoi passi, a questo punto il sistema non ha più un andamento regolare, la ruota gira alternativamente avanti ed indietro con tempi e modi irregolari, dando inizio ad un comportamento caotico evidenziato dall'attrattore di LORENZ figura sopra a destra, le linee che collegano le due spire circolari mostrano il cambio di direzione della ruota e la loro ampiezza rappresenta la diversa durata del tempo impiegata a compiere un giro.